What is an Archimedean Solid? – The following information is from Brittanica Kids with a few definitions added.
In geometry, the Archimedean solids are a special group of 13 semi-regular polyhedrons. They have a high degree of symmetry. A polyhedron is a geometric solid (three-dimensional shape) whose faces are each flat polygons. A polygon is a plane shape (two-dimensional) with straight sides such as a triangle, square, or octagon. In an Archimedean solid, the faces are regular polygons—that is, their sides are all of equal length. Additionally, an Archimedean solid has faces of two or more different types of regular polygons, such as squares and triangles. The vertices, or corners, of an Archimedean solid are all alike meaning that they are all the same angles. An Archimedean solid can be placed inside a sphere so that every vertex touches the surface of the sphere.
The ancient Greek philosopher Archimedes first described such solids. However, his works on the subject were lost and known only through other writers such as Pappus of Alexandria. Renaissance artists rediscovered several of the Archimedean solids. The Renaissance was a period in European history covering the 15th – 17th centuries (1400-1700). In 1619 the German mathematician and astronomer Johannes Kepler reconstructed the entire set of 13 and gave them Latin names.
Plato, who lived about a century before Archimedes, had described five regular solids in which all the faces are identical regular polyhedrons. These solids, now called the Platonic solids, are the tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. Some of the Archimedean solids can be thought of as variations on the Platonic solids. For example, if one starts with a cube and slices off each corner, leaving an equilateral triangle at each of the eight former corners and a regular octagon (eight-sided figure) in place of the former faces of the cube, the result is a solid with 14 faces: eight triangles and six octagons. Each vertex of the new solid brings together one of the triangles and two of the octagons. This Archimedean solid is called a truncated cube.
If one repeats the procedure but slices off the corners of the cube more deeply, so the triangles meet and only a much smaller square remains on each of the former faces of the cube, the faces of the resulting figure are eight triangles and six squares. Two triangles and two squares meet at each vertex. This is called a cuboctahedron.
Archimedean and Platonic solids are used in various kinds of modern construction such as geodesic domes because their shapes are quite stable. Most soccer balls are spherical variations on a truncated icosahedron, made up of pentagons and hexagons, with one pentagon and two hexagons meeting at each vertex.
The following is a listing of all Archimedean solids from Kiddle:
| Image | Name | Faces | Type | Edges | Vertices |
|---|---|---|---|---|---|
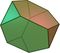 |
Truncated tetrahedron | 8 |
|
18 | 12 |
 |
Cubocthahedron | 14 |
|
24 | 12 |
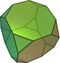 |
Truncated cube | 14 |
|
36 | 24 |
 |
Truncated octahedron | 14 |
|
36 | 24 |
 |
Rhombicuboctahedron | 26 |
|
48 | 24 |
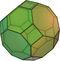 |
Truncated cuboctahedron | 26 |
|
72 | 48 |

|
Snub cube (2 mirrored versions) | 38 |
|
60 | 24 |
 |
Icosidodecahedron | 32 |
|
60 | 30 |
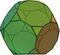 |
Truncated dodecahedron | 32 |
|
90 | 60 |
 |
Truncated icosahedron | 32 |
|
90 | 60 |
 |
Rhombicosidodecahedron | 62 |
|
120 | 60 |
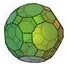 |
Truncated icosidodecahedron | 62 |
|
180 | 120 |
  |
Snub dodecahedron (2 mirrored versions) | 92 |
|
150 | 60 |
To learn even more about Archimedean Solids join us on November 25th for Advanced STEM Club where we will be making our own paper Archimedean Solids.






